Learn Matrices and Determinants with C++

$Learn Matrices and Determinants with C++$

In this article, we’ll revisit fundamental concepts about Matrices and Determinants.

Matrix

A quick explanation: a matrix organizes numeric data (like a table) to facilitate understanding and solving problems.

Matrices are used in various fields:

Mathematics;
Computing (AI, image processing…);
Engineering;
Economics;
Biology;

Among many others.

In general: A matrix is a rectangular array of numbers (or expressions) arranged in rows and columns. It looks like this:

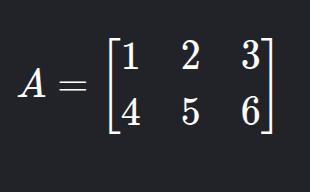
This matrix has an order of 2x3 (2 rows and 3 columns). We always start by indicating the number of rows.

The notation A = [aij]<sub>mxn</sub> means, for example:

The number 1 is in the 1st row and 1st column → a₁₁, and so on.

Converted entirely into a_ij:

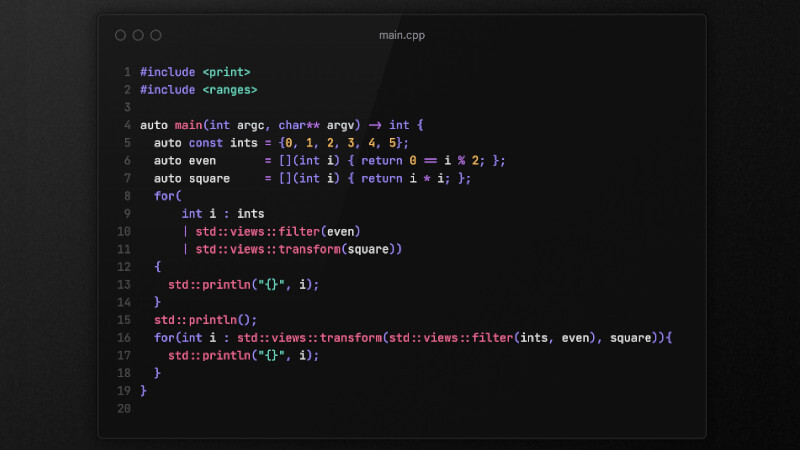
In C++, we can use std::vector or std::array:

Use std::vector<std::vector<int>> for dynamic and flexible size.
Use std::array<std::array<int, 3>, 2> for fixed size known at compile time. Never use std::list for matrices. It has inefficient random access.

Examples:

Using std::vector:

std::vector<std::vector<int>> A = {
    {1, 2, 3},
    {4, 5, 6}
};

Using std::array:

std::array<std::array<int, 3>, 2> A = { {
    {1, 2, 3},
    {4, 5, 6}
} };

Which to use?

Use std::vector if the size changes at runtime.
Use std::array for maximum performance with fixed size.

Matrix construction

Suppose you’re taking an exam and see this prompt:

Build matrix B = [a_ij]_2x3 such that a_ij = (i + j)².

Solution:

a_ij = (i + j)² ⇒ a₁₁ = (0 + 0)² ⇒ a₁₁ = 0

Do the rest accordingly

In C++, using std::array:

 
#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 3>, 2> B;

  for (int i = 0; i < 2; ++i) {
    for (int j = 0; j < 3; ++j) {
      B[i][j] = (i + j) * (i + j);
    }
  }

  for (const auto& row : B) {
    for (int val : row) {
      std::cout << val << " ";
    }
    std::cout << "\n";
  }

  return 0;
}

With std::vector, just replace:

 
std::vector<std::vector<int>> B(2, std::vector<int>(3));

The rest is the same.

The result:

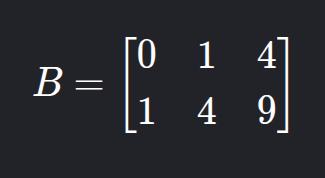
Matrix Types

Segue a tradução:

1. Square Matrix

Description: Number of rows equals number of columns (nxn).
Example:

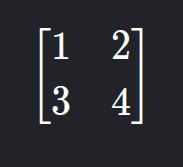
2. Row Matrix

Description: Only one row.
Example:

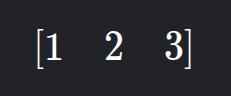
3. Column Matrix

Description: Only one column.
Example:

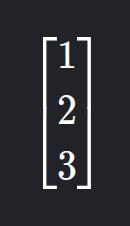
4. Zero Matrix

Description: All elements are zero.
Example:

5. Identity Matrix

Description: Main diagonal has 1s, rest are 0s. Denoted by I_n.
Example:

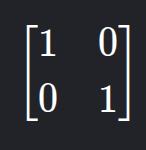
6. Diagonal Matrix

Description: Only the main diagonal can have nonzero values.
Example:

7. Scalar Matrix

Description: Diagonal matrix where all diagonal values are equal.
Example:

8. Symmetric Matrix

Description: A = A^T, i.e., equal to its transpose.
Example:

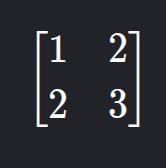
9. Skew-Symmetric Matrix

Description: A^T = -A. Main diagonal is always zero.
Example:

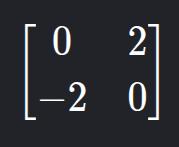
10. Upper Triangular Matrix

Description: All elements below the main diagonal are zero.
Example:

11. Lower Triangular Matrix

Description: All elements above the main diagonal are zero.
Example:

12. Transpose Matrix

Description: Rows become columns. Denoted A^T.
Example:

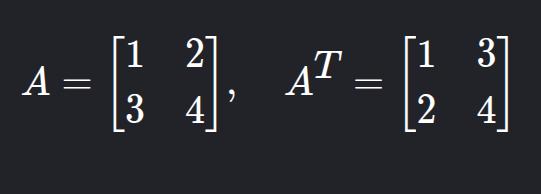
13. Opposite Matrix

Description: All elements multiplied by -1.
Example:

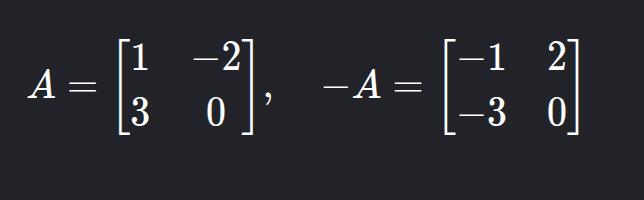
14. Rectangular Matrix

Description: Number of rows is different from number of columns.
Example:

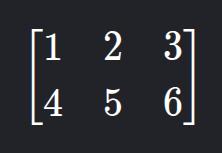
Matrix Calculations

Arithmetic (algebraic or matrix) operations with matrices.

a) Addition and Subtraction

Only possible if matrices have the same order.

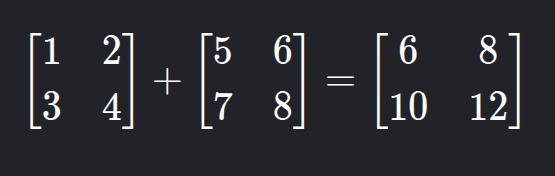
That is, 1 + 5 = 6, 2 + 6 = 8, and so on.

In C++:

#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B = { { {5, 6}, {7, 8} } };
  std::array<std::array<int, 2>, 2> C;

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      C[i][j] = A[i][j] + B[i][j];
    }
  }

  for (auto& row : C){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

b) Scalar Multiplication

Each element is multiplied by a real number (scalar).

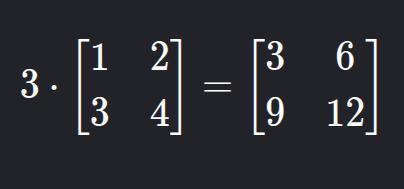
That is, 3 x 1 = 3, 3 x 2 = 6, and so on.

In C++:

#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B;
  int scalar = 3;

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      B[i][j] = scalar * A[i][j];
    }
  }

  for (auto& row : B){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

c) Matrix Multiplication

The number of columns of the first matrix must equal the number of rows of the second.

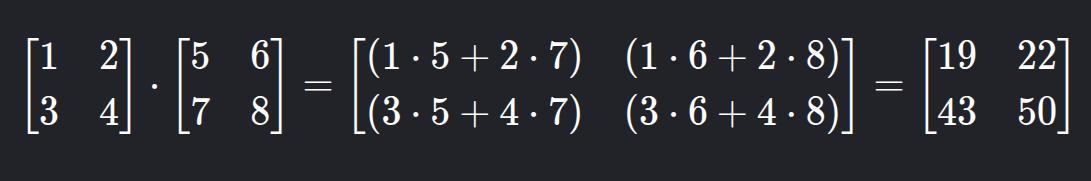
In C++:

#include <array>
#include <iostream>

int main() {
  std::array<std::array<int, 2>, 2> A = { { {1, 2}, {3, 4} } };
  std::array<std::array<int, 2>, 2> B = { { {5, 6}, {7, 8} } };
  std::array<std::array<int, 2>, 2> C = {};

  for (int i = 0; i < 2; ++i){
    for (int j = 0; j < 2; ++j){
      for (int k = 0; k < 2; ++k){
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }

  for (auto& row : C){
    for (int v : row){
      std::cout << v << (v == row.back() ? '\n' : ' ');
    }
  }
}

Determinants

A determinant is a number associated only with square matrices, useful to solve linear systems and verify if a matrix is invertible.

IMPORTANT: Matrices are denoted with brackets [ ], but determinants use vertical bars | |.

3.2 Calculating the Determinant

a) `2x2` Matrix

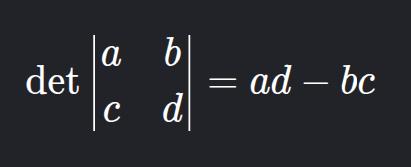
Example:

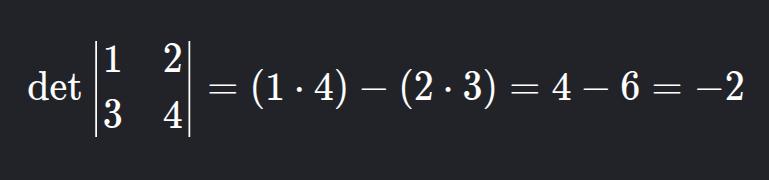
Em C++:

 
#include <iostream>

int main(){
  int a = 1, b = 2;
  int c = 3, d = 4;

  int det = a * d - b * c;

  std::cout << det << '\n';
}

b) `3x3` Matrix (Sarrus Rule)

Sarrus’ Rule consists of appending the 1st and 2nd columns to the right side of the determinant matrix and drawing diagonals (starting from the numbers in the first ROW), for example:

This is for a 3x3 matrix.

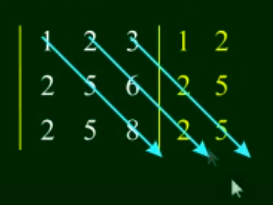
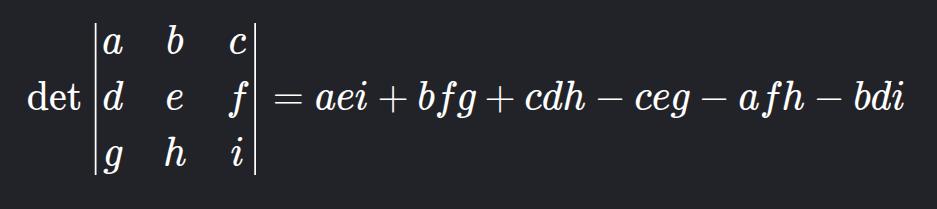
Example:

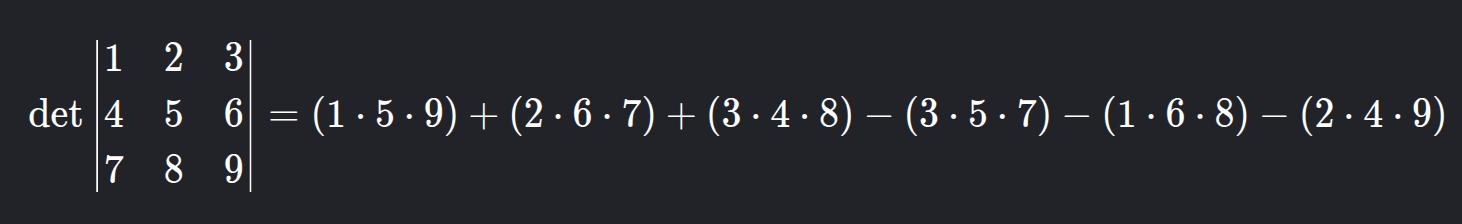
= 45 + 84 + 96 - 105 - 48 - 72 = 0

In C++:

#include <iostream>

int main(){
    int a11 = 1, a12 = 2, a13 = 3;
    int a21 = 4, a22 = 5, a23 = 6;
    int a31 = 7, a32 = 8, a33 = 9;

    int det =
        a11 \* a22 \* a33 +
        a12 \* a23 \* a31 +
        a13 \* a21 \* a32
        \- a13 \* a22 \* a31
        \- a11 \* a23 \* a32
        \- a12 \* a21 \* a33;

    std::cout << det << '\n';
}

3.3 Properties of Determinants

If a row or column is all zeros, det = 0.
If two rows or columns are equal, det = 0.
det(A x B) = det(A) x det(B).

4. Applications

Linear Systems: Solve using Cramer’s Rule.
Inverse Matrix: A matrix A is invertible if det(A) ≠ 0.

5. Exercise

Compute the determinant:

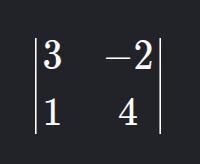
Em C++:

 
#include <iostream>

int main(){
  int a = 7, b = 3;
  int c = -2, d = 4;

  int det = a * d - b * c;

  std::cout << det << '\n';
}

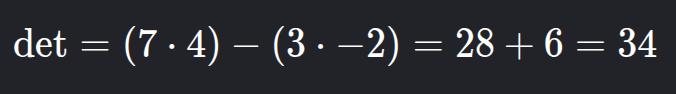
Answer: 14.

math cpp